2. 图像卷积

1. 卷积运算 → 互相关运算 (cross-correlation)

• 二维互相关：
  • 定义：将输入和核矩阵进行交叉相乘，加上偏移后得到输出。
  • 示例：

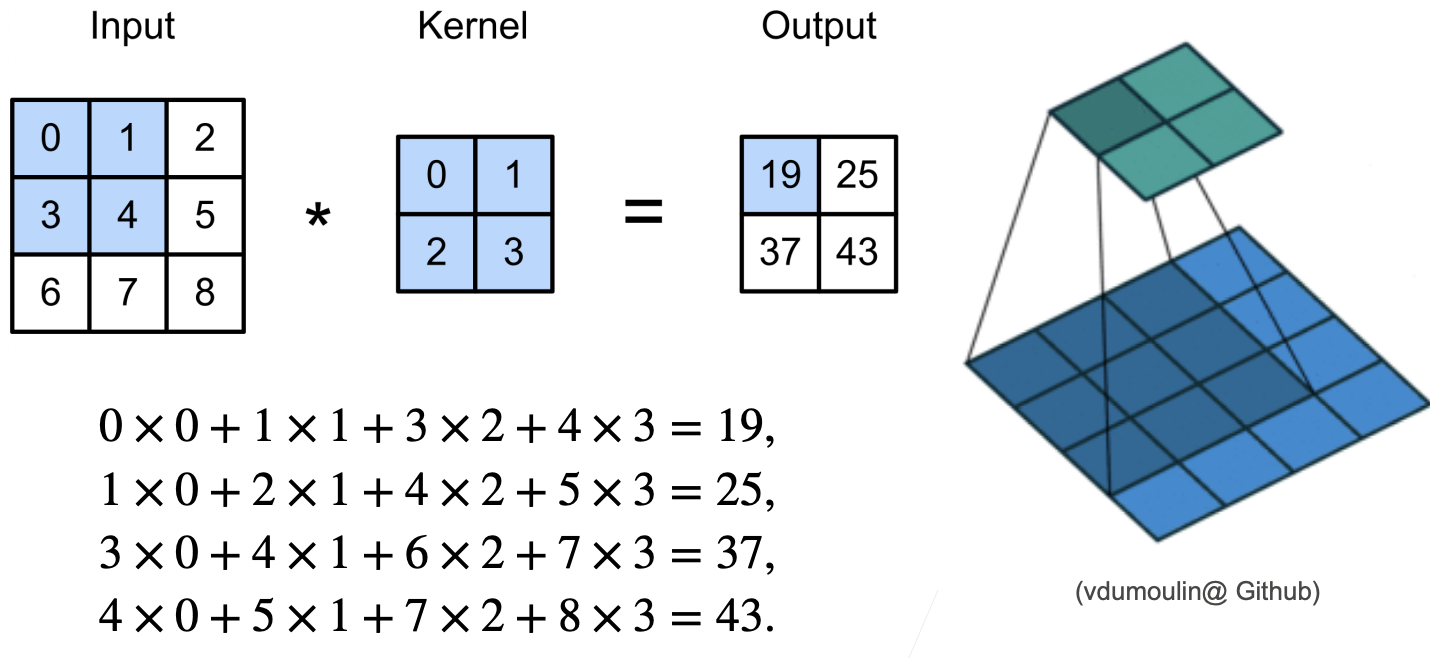
2. 输入输出尺寸

• 输入 $X$：大小为 $n_h\times n_w$（超参数）。
• 核 (kernel) $W$：大小为 $k_h\times k_w$。
• 偏置 $b\in \mathbb{R}$。
• 输出 $Y$：大小为 $(n_h-k_h+1)\times (n_w-k_w+1)$。
  • 原因：核滑动时，边缘位置无法完全覆盖输入，导致输出尺寸缩小。
    
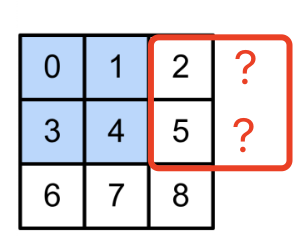
  • 如图，扫到这里没了，所以不输出，导致丢掉一些数据，就是$(-k_h+1)$ 和 $(-k_w+1)$ 就会导致一下结果，图片变模糊
    
• 公式：$Y=X\ast W+b$，其中 $W$ 和 $b$ 是可学习参数。

3. 互相关 vs. 卷积

• 互相关：

  $$y_{i,j}=\sum _{a=1}^{k_h}\sum _{b=1}^{k_w}{W}_{a,b}\cdot X_{i+a,j+b}$$

• 卷积：

  $$y_{i,j}=\sum _{a=1}^{k_h}\sum _{b=1}^{k_w}{W}_{k_h-a+1,k_w-b+1}\cdot X_{i+a,j+b}$$

• 区别：卷积需要对核做180°翻转。对于对称核（如高斯核），两者结果相同。深度学习中通常采用互相关实现。

4. 一维与三维互相关

• 一维互相关（如文本/时间序列）：

  $$y_i=\sum _{a=1}^k{W}_a\cdot X_{i+a}$$

• 三维互相关（如视频、医学影像）：

  $$y_{i,j,k}=\sum _{a=1}^{k_h}\sum _{b=1}^{k_w}\sum _{c=1}^{k_d}{W}_{a,b,c}\cdot X_{i+a,j+b,k+c}$$

5. 总结

• 核心思想：通过滑动小尺寸核，对输入局部区域加权求和，实现特征提取与参数量压缩。
• 关键参数：核大小、步长、填充（padding）。

参考资料

• 动手学深度学习 6.2：图像卷积层
• Bilibili：图像卷积